
17.01.2024

17.01.2024
Цель работы – идентификация шоковых событий и анализ их влияния на рынок публичных вакансий рабочих. Российский рынок труда в 2023 г. находится в процессе структурной перестройки с связи c дефицитом работников, поэтому проблема разработки подхода для анализа изменения структуры спроса на рынке публичных вакансий является особенно актуальной. Гипотеза исследования состоит в том, что поведение работодателей на рынке публичных вакансий рабочих можно описать действиями одного рационального репрезентативного агента. Методом исследования является математическое моделирование с помощью непараметрического метода построения экономических индексов. В результате работы был получен подход для определения периодов времени, несогласованных со сложившейся структурой спроса, а также способ для оценки степени завышения предлагаемой зарплаты после начала пандемии.
Начало пандемии, введение локдауна и режима нерабочих дней остро отразилось на предприятиях, деятельность которых не предполагает удаленного режима работы сотрудников. Заражение сотрудников коронавирусной инфекцией COVID-19 и выход на больничный не позволило предприятиям эффективно продолжить работу в прежнем режиме. Очевидно, что данные события повлияли на российский рынок труда, а проблемы его транс формации в период шоковых событий представляют большой интерес для принятия социально-экономических решений.
Одним из индикаторов ситуации на рынке труда являются публичные вакансии, которые отражают спрос работодателей на дополнительную потребность в работниках. Данная работа посвящена исследованию рынка публичных вакансий на основе данных автоматизированной информационной системы (АИС) «Мониторинг рынка труда» ФГБУ «ВНИИ труда» Минтруда России. АИС сводит и агрегирует первичную информацию с трех ключевых российских рекрутинговых он лайн-платформ, размещающих актуальные объявления о вакансиях в разных регионах Российской Федерации: «Работа России», «HeadHunter», «Superjob». На сентябрь 2023 г. содержит более 68 млн вакансий, опубликованных в период с января 2018 г. по август 2023 г.
Собранные вакансии проходят идентификацию и разметку по ключевым параметрам, в том числе тип занятости, требуемый опыт, принадлежность к типовой позиции. При обработке со бранных массивов производится дедубликация вакансий – исключение из анализа повторных публикаций объявлений о найме, фактически от носящихся к одному вакантному рабочему месту. Для анализа выбрана группа типовых позиций рабочих, поскольку для сотрудников таких профессий нет возможности удаленной работы. Данные представлены в виде помесячного набора количества требуемых вакансий и медианы нижней границы (поле «Заработная плата ОТ» вакансий) предлагаемой заработной платы типовых позиций рабочих в профессионально-квалификационном и региональном разрезе с 2018 по 2023 гг.
Удобным инструментом агрегации для анализа статистики в разрезе широкой номенклатуры является построение экономических индексов для групп укрупненного классификатора. Но стандартные подходы к вычислению индексов такие, как индексы Ласпейреса или Пааше, не учитывают эффекты замещения и изменения структуры спроса, поскольку используют для своего расчета фиксированную потребительскую корзину в базовый или текущий момент времени. Указанную проблему решает непараметрический метод построения экономических индексов Конюса-Дивизиа.
Непараметрический метод основан на теории выявленного предпочтения и позволяет проверять согласованность потребительского поведения с моделью спроса Парето [1, 2]. Согласно модели Парето спрос совокупности домашних хозяйств можно описать с помощью рассмотрения одного рационального репрезентативного агента, максимизирующего свою функцию полезности F при заданных бюджетных ограничениях. Возникающая при этом задача называется прямой за дачей в модели Парето. Обратная задача Парето заключается в нахождении функции полезности F из некоторого класса функций Ф при известных обратных функциях спроса P(X) такой, чтобы лю бой вектор X ≥ 0 являлся решением задачи:
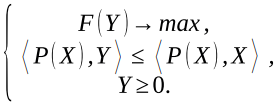
Если последняя задача имеет решение, то об ратные функции спроса называются рационализируемыми в классе функций Ф. Однако задача не всегда может иметь решение, поэтому в работе [3] был разработан обобщенный непараметрический метод путем введения показателя нерациональности и алгоритма для его вычисления. Метод позволяет строить экономические индексы Конюса-Дивизиа для статистик, несогласованных с моделью Парето.
Обобщенный непараметрический метод широко применяется для анализа сегментации потребительского рынка [4], для этого вводится понятие отделимости товарных подгрупп. Каждая отделимая подгруппа образует независимый сегмент товарного рынка, который можно рассматривать отдельно от остальных товаров. Свойства отделимости являются важной структурной характеристикой потребительского спроса. Проблемы анализа отделимости исследуются в работах [5, 6]. Также обобщенный непараметрический метод используется для идентификации периодов структурных изменений в исследуемой группе [4, 7].
В рамках данного исследования обобщенный непараметрический метод применен для анализа статистики рынка публичных вакансий. В результате определены периоды, в которые происходи ли изменения на рынке публичных вакансий рабочих, изучена реакция рынка на них, проведена оценка во сколько раз предлагаемая заработная плата была завышена после начала пандемии, а также построены индексы предлагаемой зарплаты и количества вакансий для выделенных сегментов вакансий рабочих.
Непараметрический метод построения экономических индексов был предложен А.А. Шананиным в 1993 г. [8] и основан на теореме Африата-Вериана [9-11]. Метод позволяет проверять согласованность наблюдаемого потребительского поведения с моделью одного рационального репрезентативного агента, который максимизирует свою функцию полезности при заданных бюджетных ограничениях. При этом функция полезности репрезентативного агента выбирается из класса положительно-однородных функций, что бы она была инвариантна относительно масштабов, т.е. при кратном росте объема потребляемых товаров значение функции пропорционально увеличивается. Для применения метода необходимы статистические данные – временные ряды {(Pt, Xt)}t=0T, где Рt – вектор цен, составленный из совокупности цен на выделенные товары в пери од времени t, а Xt - вектор спроса на эти товары при ценах, установившихся в период времени t. Если для статистики существует функция полезности из заданного класса, которая отражает по ведение выделенного рационального агента, то такая статистика называется рационализируемой в этом классе функций. Рационализируемость статистики влечет за собой возможность построения индексов цен и объемов Конюса-Дивизиа.
Однако наблюдаемые статистические данные не всегда можно описать действиями одного рационального репрезентативного агента, а значит
нельзя построить индексы. Во-первых, это может быть связано с погрешностями, неизбежно существующими при формировании статистики. Как правило, статистика не содержит полной ин формации об исследуемом рынке, часть данных не попадают в систему сбора статистики. Кроме того, данные приходят в агрегированном виде, что может служить дополнительным источником ошибок. Во-вторых, на рынке могут происходить изменения предпочтений потребителей под влиянием внешних шоковых событий, таких как пандемия. Механизмы поведения потребите лей изменяются, что может привести как к новой сложившейся структуре на исследуемом рынке, так и быть временным отклонением. В-третьих, анализируемый рынок может характеризоваться несколькими группами потребителей с различными предпочтениями. В таком случае корректно использовать модели нескольких рациональных репрезентативных потребителей.
Вопрос введения показателя, измеряющего степень рационализируемости статистики рассматривался в работах [3, 10, 12, 13]. Введение поправочного параметра ω расширяет возможности для построения экономических индексов. Минимальный параметр ω≥1, при котором статистика становится рационализируемой, называется по казателем нерациональности статистики. Показатель нерациональности отражает степень согласованности статистики с моделью рационального репрезентативного агента, а также служит мерой погрешности, принимаемой при построении индексов Конюса-Дивизиа. Чем выше показатель нерациональности, тем хуже построенные индексы демонстрируют реальную динамику цен и объемов для агрегируемой группы товаров. Метод построения индексов с введением показателя нерациональности ω≥1 называется обобщенным непараметрическим.
Обобщенный непараметрический метод позволяет решать задачу сегментации потребительского спроса (см. пример в [4]). Для этого важно ввести понятие отделимой подгруппы. Пусть за дана статистика из m товаров, и она согласована с моделью Парето одного рационального репрезентативного потребителя, т.е. рационализируема. Подгруппа из n<m товаров называется отделимой, если выполнены следующие условия:
Формально, это значит, что функция полезности репрезентативного потребителя всех товаров F представима в виде F(X)=F0(F1(X1),X2), где X – век тор объемов потребления всех товаров, X1 – вектор объемов потребления товаров отделимой подгруппы, X2 – вектор объемов потребления остальных товаров, F1 – функция полезности репрезентативного потребителя товаров этой подгруппы, а F0 – некоторая функция полезности из того же класса положительно-однородных функций, из которого функции F1 и F.
На основе обобщенного непараметрического метода в статье [7] был предложен метод для определения пар периодов, которые вносят наибольший вклад в величину показателя нерациональности. Предлагается задать нормальный уровень показателя нерациональности, его логарифм обо значим Ω* ≥ 0 . В результате применения метода получается ориентированный граф, вершинами которого выступают периоды времени рассматриваемой статистики. Утверждается, что исключение всех ребер графа путем исключения вершин-периодов времени приведет к снижению показателя нерациональности ниже уровня Ω* ≥ 0. Такая процедура позволяет выделить небольшое количество временных точек, статистика за которые не согласована с остальной статистикой, а значит в выделенные моменты времени происходили события, приведшие к отклонению наблюдаемой статистики от модели одного рационального репрезентативного агента. Описанный прием будем называть методом выделения несогласованных пар периодов.
Стоит отметить, что обобщенный непараметрический метод и его модификации могут быть применимы не только для анализа статистики, связанной с потребительским спросом. Метод позволяет исследовать структуру обратных функций спроса, т.е. зависимость рыночных объемов потребления от наблюдаемых цен. Такая связь присутствует и на рынке публичных вакансий. Потребителем на рынке публичных вакансий выступает работодатель, имеющий спрос на дополнительную рабочую силу, и он вынужден выставлять предлагаемую зарплату в соответствии с рыночным уровнем. Количество вакансий и предлагаемые зарплаты в разрезе типовых позиций можно интерпретировать как вектор объемов и вектор цен. Поэтому метод, разработанный для анализа потребительского спроса, корректно применять и для анализа изменений на рынке труда. В данной работе в качестве входных данных будет использоваться статистика рынка публичных вакансий {(Pt, Xt)}t=0T – временные ряды совокупности вектора предлагаемой заработной платы и вектора количества вакансий при заданной зарплате.
Под справедливым уровнем предлагаемой заработной платы в данном исследовании пони мается уровень предлагаемой работодателями зарплаты, согласованный со сложившейся структурой спроса на рынке. С помощью обобщенного непараметрического метода можно прогнозировать уровень предлагаемой заработной платы при заданном количестве вакансий в некоторый период времени. Прогноз уровня предлагаемой заработной платы основан на гипотезе, что в рассматриваемый период предпочтения работодателей на рынке публичных вакансий остались прежними и описываются действиями одного рационального репрезентативного агента.
Пусть имеется статистика публичных вакансий S = {(Pt, Xt)}t=1T, рационализируемая с по казателем нерациональности ω≥1. Необходимо предсказать вектор предлагаемой зарплаты Pθ при заданном количестве вакансий Xθ, чтобы рас ширенная статистика SU{(Pθ, Xθ)} также была рационализируема с показателем нерациональности ω. Обозначим Ctτ = ⟨Pτ, Xτ⟩ / ⟨Pt, Xτ⟩ – матрицу индексов цен Пааше, где ⟨⋅ , ⋅ ⟩ – скалярное произведение двух векторов. В [8] было получено, что множество таких векторов Pθ задается системой линейных неравенств:
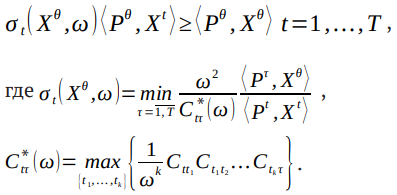
(1)
Подход позволяет оценить справедливый уровень предлагаемой зарплаты в периоды изменений на рынке публичных вакансий. Различие между наблюдаемой предлагаемой зарплатой и полученной оценкой стоит интепретировать как премию работникам за трудоустройство и работу в условиях шоковых событий.
Далее в данной работе проводился анализ вакансий для регионов со средним уровнем доходов населения. Разбивка регионов РФ на 3 группы по уровню доходов приведена в программном комплексе. В средней группе регионов проживает 54% всего населения РФ, в этой группе регионов широко представлен рабочий класс. В рамках исследования оказалось важным рассматривать вакансии вахтовых рабочих отдельно от вакансий, предлагающих работу стандартным методом, так как предлагаемая зарплата в месяц на вахте более высокая, что может быть связано с более длинной продолжительностью рабочего дня и недели.
Для анализа без учета вахты были выбраны 11 востребованных типовых позиций рабочих:
Логарифм показателя нерациональности всей статистики равен ω=0.034. Здесь и далее в данной работе в качестве показателя нерациональности имеется в виду его логарифм, поэтому далее считаем, что ω>0.
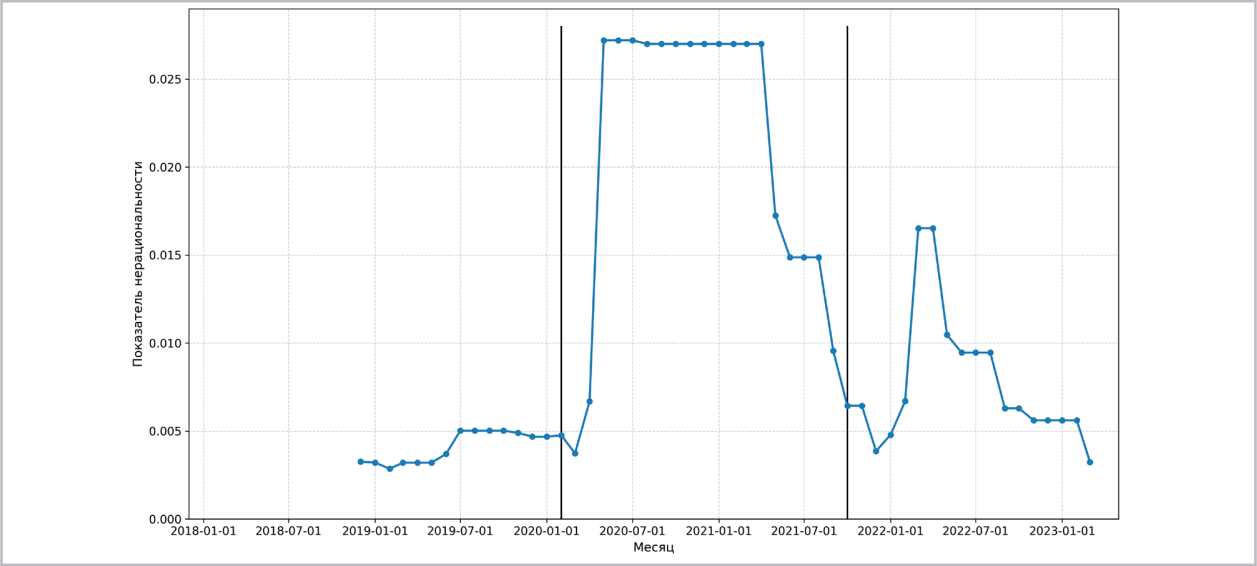
Рис. 1 / Fig. 1. Показатели нерациональности статистики вакансий рабочих с опытом работы от 1 года до 3 лет, рассчитанные методом скользящего окна шириной 12 месяцев. По оси абсцисс откладываются правые границы промежутков, за которые рассчитаны показатели нерациональности / Irrationality indices for the statistics of vacancies of workers with work experience from 1 to 3 years, calculated by the sliding window method of 12 months width. The x-axis shows the right boundaries of the intervals for which the irrationality indices are calculated.
Источник / Source: составлено авторами / compiled by the authors.
С помощью обобщенного непараметрического метода для скользящего временного диапазона шириной 12 месяцев была построена динамика показателя нерациональности для статистики публичных вакансий рабочих с опытом работы 1-3 года без учета вахты (рис. 1). Начало и конец диапазона последовательно сдвигались на 1 месяц вперед, а на график наносился логарифм показа теля нерациональности статистики за 12 месяцев в зависимости от правой границы временного диапазона. На рис. 1 виден резкий рост показателя нерациональности с начала пандемии в РФ, в мае 2020 г., а также скачок в марте 2022 г. Как только в рассматриваемый диапазон попадает май 2020 г., показатель нерациональности статистики вырастает до уровня 0.027. Это означает, что статистика за указанный промежуток плохо согласуется с моделью одного рационального репрезентативного агента, что дает основания для более детального исследования изменений, произошедших после начала пандемии.
Временной диапазон всей статистики разбивается на три периода: допандемийный – c января 2018 г. по февраль 2020 г., пандемийный – с
марта 2020 г. по октябрь 2021 г. и послепандемийный – с ноября 2021 г. по март 2023 г.
Последовательно выделим периоды, вносящие большой вклад в показатель нерациональности статистики. Для этого воспользуемся методом выделения несогласованных пар периодов.
Если задать нормальный уровень показателя нерациональности Ω* ≥ 0 = 0.025 и применить указанный метод, получается ориентированный граф, изображенный на рис. 2.
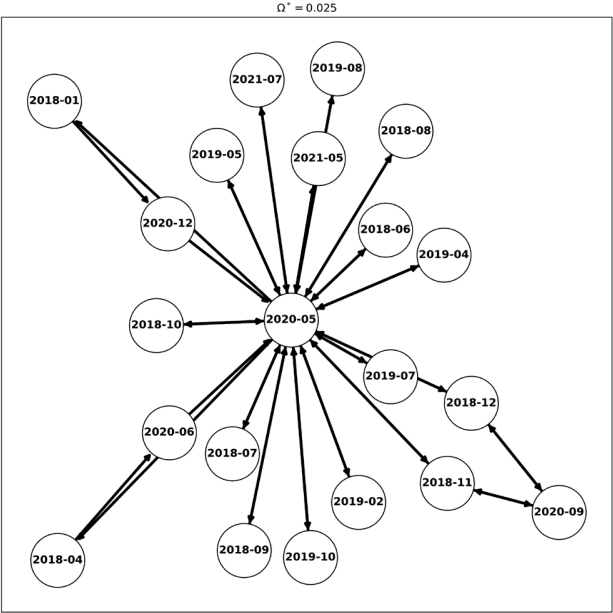
Рис. 2 / Fig. 2. Граф несогласованных пар периодов для статистики вакансий рабочих с опытом работы от 1 года до 3 лет / Graph of inconsistent pairs of periods for statistics of vacancies of workers with work experience from 1 to 3 years.
Источник / Source: составлено авторами / compiled by the authors.
Вершинами графа являются месяцы исходной статистики, а ребра между вершинами указывают на несогласованность между месяцами с точки зрения гипотезы рационального репрезентативного агента. Для исключения всех ребер графа достаточно исключить всего лишь четыре вершины: май, июнь, сентябрь и декабрь 2020 г., а значит исключение этих периодов из статистики должно привести снижению показателя нерациональности стати стики до уровня Ω* ≥ 0.
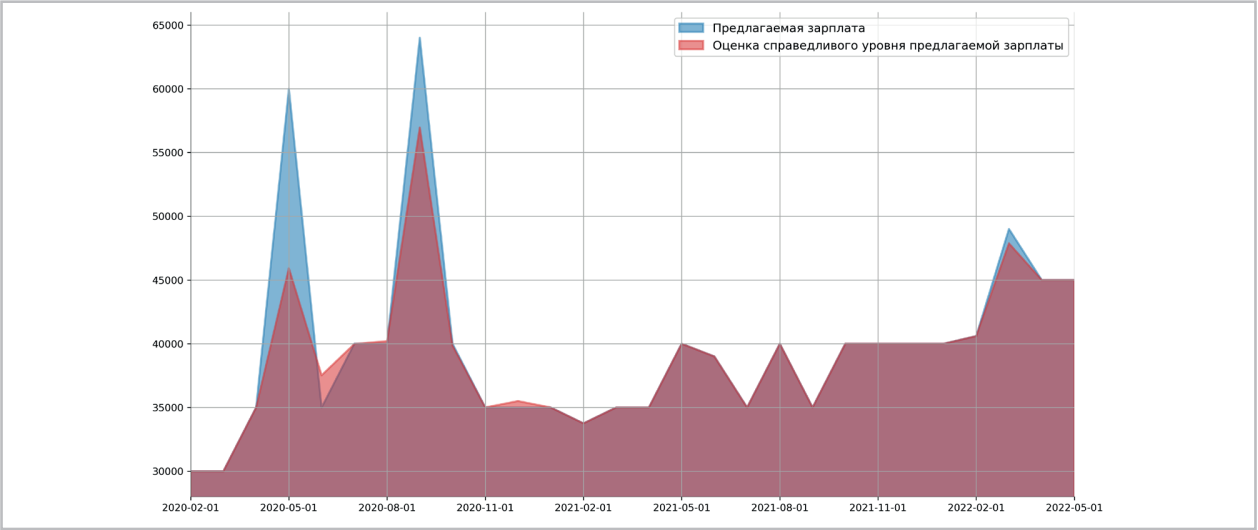
Рис. 3 / Fig. 3. Оценка справедливого уровня нижней границы предлагаемой зарплаты для токарей с опытом работы от 1 года до 3 лет / Estimation of the fair level of the lower limit of the proposed salary for turners with work experience from 1 to 3 years.
Источник / Source: составлено авторами / compiled by the authors.
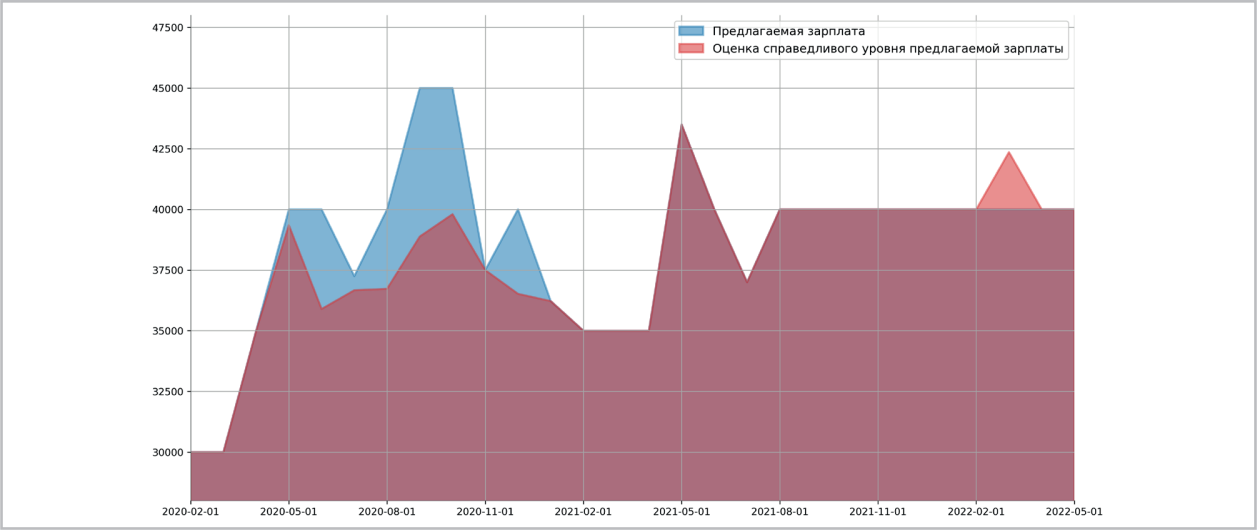
Рис. 4 / Fig. 4. Оценка справедливого уровня нижней границы предлагаемой зарплаты для сварщиков с опытом работы от 1 года до 3 лет / Estimation of the fair level of the lower limit of the proposed salary for welders with work experience from 1 to 3 years.
Источник / Source: составлено авторами / compiled by the authors.
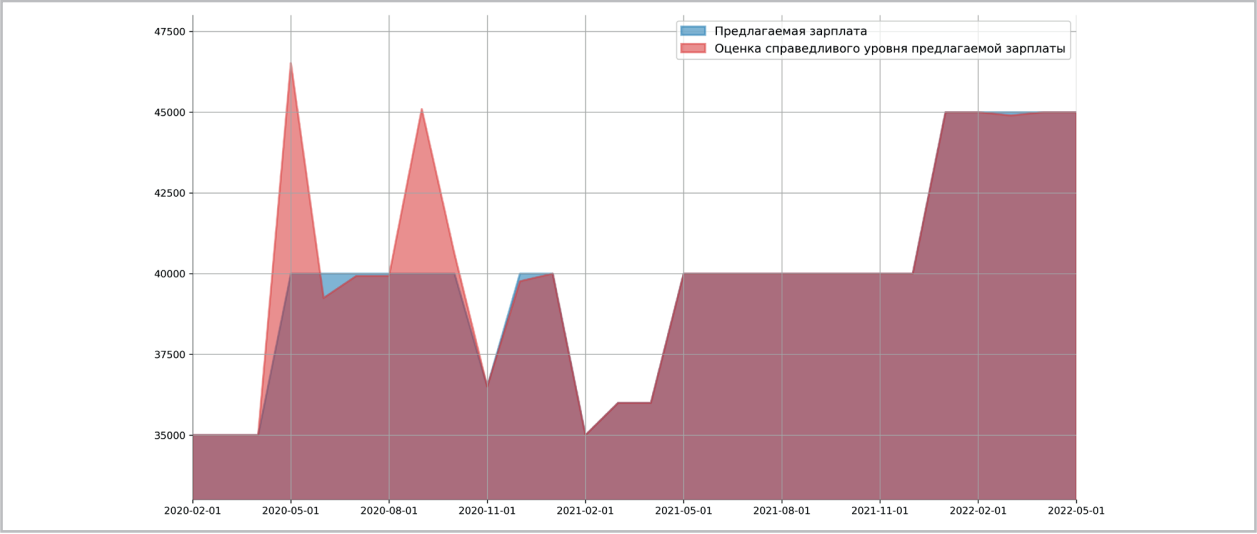
Рис. 5 / Fig. 5. Оценка справедливого уровня нижней границы предлагаемой зарплаты для операторов станка с ЧПУ с опытом работы от 1 года до 3 лет / Estimation of the fair level of the lower limit of the proposed salary for CNC machine operators with work experience from 1 to 3 years.
Источник / Source: составлено авторами / compiled by the authors.
Действительно, после исключения показатель нерациональности статистики снизился с ω=0.034 до 0.024. Постепенно понижая нормальный показатель нерациональности и применяя метод выделения несогласованных пар периодов, можно выбрать периоды, исключение которых приводит к дальнейшему снижению показателя нерациональности исходной стати стики. Оказалось, что исключение из статистики периодов с мая по октябрь 2020 г., декабря 2020 г. и марта 2022 г. снижает показатель нерациональности статистики до уровня ω=0.012. В результате группу вакансий рабочих без вахты с требуемым опытом от 1 года до 3 лет можно считать рационализируемой, а высокое значение показателя нерациональности связано с началом пандемии.
В результате анализа исходных данных был выявлен резкий рост нижней границы предлагаемой зарплаты в выделенные периоды. Поэтому возникла задача оценки справедливого уровня предлагаемой заработной платы, исходя из гипотезы рационального репрезентативного агента.

(2)
Задача (2) является задачей квадратичного программирования и заключается в нахождении вектора предлагаемых зарплат с положительны ми компонентами – предлагаемыми зарплатами типовым позициям рабочих. При этом для решения задачи должно быть выполнено условие (1), т.е. добавление к статистике временной точки со скорректированной зарплатой не должно приводить к повышению показателя нерациональности выше нормального уровня Ω*. Минимизируемый функционал говорит о том, что оценка зарплаты должна быть близка к наблюдаемому вектору предлагаемых зарплат.
Последовательно решив задачу (2) по отдельности для периодов θ с мая по октябрь 2020 г., декабря 2020 г. и марта 2022 г., были получены оценки нижней границы справедливого уровня предлагаемой зарплаты рабочих (рис. 3–5).
Согласно модели нижняя граница предлагаемой зарплаты для токарей завышена на 30% в мае 2020 г.: c 46 тыс. до 60 тыс. рублей, на 12% в сентябре 2020 г.: с 57 тыс. до 64 тыс. рублей (рис. 3). Для сварщиков нижняя граница предлагаемой зарплаты в сентябре 2020 года завышена на 15,7%: c 38,9 тыс. до 45 тыс., а в марте 2022 г. занижена на 5,6%: на 2,4 тыс. руб. (рис. 4). При этом наблюдается занижение предлагаемой зарплаты для опера торов станка с ЧПУ до 15% (рис. 5). Для остальных типовых позиций рабочих оценка справедливого уровня предлагаемой зарплаты после начала пандемии близка к наблюдаемым значениям в стати стике.
После оценки уровня предлагаемой зарплаты снизились показатели нерациональности для вы деленных периодов статистики: для пандемийного периода с марта 2020 г. по октябрь 2021 г. показатель нерациональности ω=0.028 снизился до 0.012, для послепандемийного – с ω=0.006 до ω=0.005. Показатель нерациональности допандемийного периода остался равен ω=0.005. Показатель нерациональности всей статистики снизился до уровня ω=0.012.
В итоге помощью обобщенного непараметрического метода построения индексов была про ведена оценка степени завышения предлагаемой зарплаты рабочим, в связи с возросшим спросом на рабочих стандартным методом работы после начала пандемии в России. Этот результат может быть полезен для планирования фонда оплаты труда на дополнительную рабочую силу в условиях дефицита специалистов на рынке.
Статистика вакансий рабочих вахтовым методом имеет показатель нерациональности ω=0.066, что примерно в два раза выше, чем для группы типовых позиций без учета вахты ω=0.034. Исключение несогласованных периодов позволило снизить показатель нерациональности статистики только до уровня 0.04, а для достижения приемлемого уровня 0.02 необходимо исключить много периодов, не связанных между собой. Делаем вывод, что группа вакансий рабочих на вахте с опытом 1-3 года нерационализируема, и при этом избыточную нерациональность нельзя объяснить изменениями в конкретные промежутки времени.
Далее интересно изучить взаимосвязь публичных вакансий вахтовым методом и стандартным методом для рабочих с требуемым опытом от 1 года до 3 лет.
Были проанализированы две модели. В первой рассмотрены 18 типовых позиций: 11 типовых позиций рабочих без вахты и 7 типовых позиций на вахте. Показатель нерациональности такой статистики ω=0.096. Исключение периодов с мая по октябрь 2020 г., декабря 2020 г., марта и апреля 2022 г. и периода с января по март 2023 г. позволяет снизить показатель нерациональности до уровня ω=0.025.

Рис. 6 / Fig. 6. Модель рынка публичных вакансий рабочих с опытом от 1 года до 3 лет/ Model of the public vacancy market for workers with work experience from 1 to 3 years.
Источник / Source: составлено авторами / compiled by the authors.
Однако, как было получено ранее, группу типовых позиций рабочих без вахты с опытом работы от 1 года до 3 лет можно считать рационализируемой, а значит корректно рассматривать индекс этой группы среди типовых позиций рабочих на вахте. Во второй модели была рассмотрена статистика из 8 позиций: 7 типовых позиций рабочих на вахте и одной позиции-индекса рабочих без вахты:
Показатель нерациональности такой стати стики ω=0.085. Исключением периодов c мая по октябрь 2020 г., с марта по апрель 2022 г., января 2023 г. и марта 2023 г. удается снизить показатель нерациональности до уровня ω=0.026. Получаем, что группа вакансий рабочих со стандартным методом работы и требуемым опытом работы от 1 года до 3 лет отделима от группы всех публичных вакансий рабочих с аналогичным опытом. Вторая модель видится предпочтительной (рис. 6).
Поведение предприятий на рынке публичных вакансий рабочих с опытом от 1 года до 3 лет без вахты описывается действиями одного рационального репрезентативного агента. Значит, группа типовых позиций рабочих без вахты составляет группу взаимозаменяемых и взаимодополняемых вакансий. Работник с опытом работы от 1 года до 3 лет имеет возможность сменить одну профессию на другую после приобретения требуемых навыков. Если работник рассматривает вахтовый метод как вариант трудоустройства, то среди вахтовых типовых позиций у него имеется альтернатива в виде отделимой группы рабочих со стандартным методом работы.
Ниже построены графики динамики индексов предлагаемой зарплаты (рис. 7) и индекса количества вакансий (рис. 8) для отделимой группы типовых позиций рабочих с опытом от 1 года до 3 лет со стандартным методом работы и для всех позиций.
С начала 2018 г. нижняя граница предлагаемой зарплаты рабочим выросла в 2 раза, с 24 тыс. до 50 тыс. руб., для стандартного метода работы и в среднем с 30 тыс. до 60 тыс. руб. для всех методов работы. При этом стремительно растет спрос на рабочих, начиная с ноября 2019 г., в первую очередь благодаря вакансиям на вахте. После начала пандемии, с мая по октябрь 2020 г., резко выросла потребность в дополнительной рабочей силе стандартным методом. Заболевшие рабочие были вынуждены уйти в карантин, а предприятиям было необходимо срочно найти работников на их ме ста. Резко возросший спрос на рабочих при ограниченном предложении сопровождался ростом предлагаемой зарплаты до уровня, предлагаемо го на вахте. Стоит отметить, что трудоустройство сотрудников вахтовым методом становится все более популярным среди работодателей: с марта 2021 г. более половины всех вакансий рабочих с опытом от 1 года до 3 лет приходятся на вахту, а в апреле 2022 г. доля вакансий на вахте достигала 70%. В мае 2021 г. наблюдается провал в спросе на рабочих, его можно объяснить нерабочими майскими праздниками с 1 по 10 мая в связи с ростом заболеваемости в рамках пандемии. За короткий рабочий месяц предприятия снизили активность по найму. Предприятия, которым срочно требовались рабочие, были вынуждены повышать уровень предлагаемой зарплаты.
В данном разделе изучалась взаимосвязь вакансий рабочих с различным опытом работы и с разным методом трудоустройства: вахтовым или стандартным методом работы.
В ходе анализа оказалось, что статистика рынка публичных вакансий рабочих без опыта работы рационализируема с низким показателем нерациональности ω=0.021. Выделение несогласованных периодов для снижения ω не привело ни к какому результату.
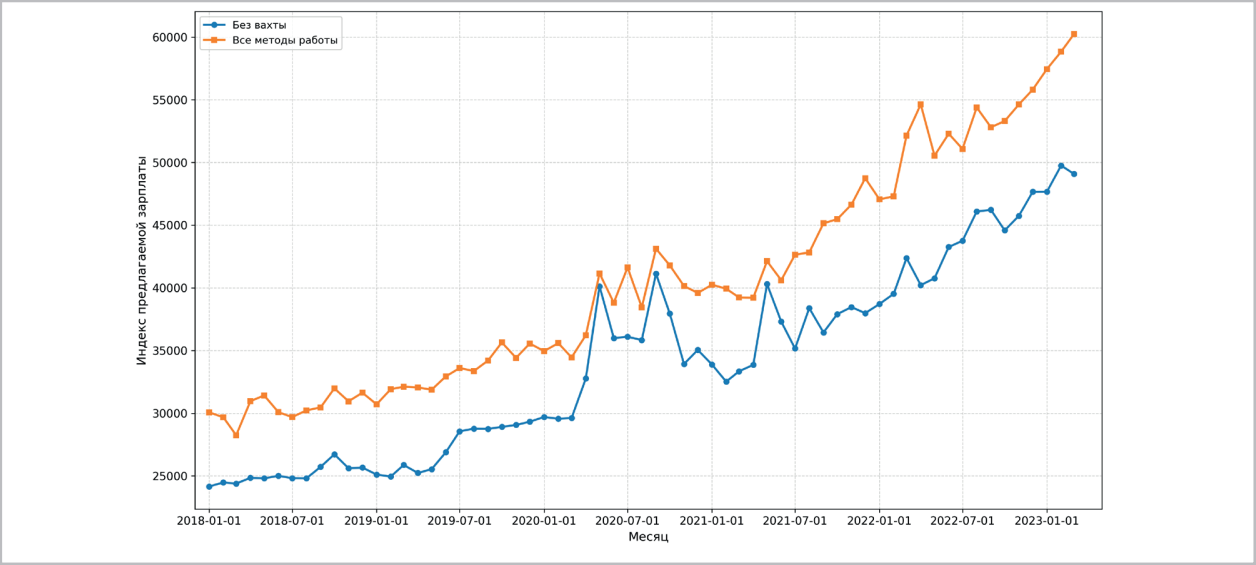
Рис. 7 / Fig. 7. Индекс нижней границы предлагаемой зарплаты для рабочих с опытом работы от 1 года до 3 лет / Index of the lower limit of the proposed salary for workers with work experience from 1 to 3 years.
Источник / Source: составлено авторами / compiled by the authors.

Рис. 8 / Fig. 8. Индекс количества вакансий для рабочих с опытом работы от 1 года до 3 лет / Index of the number of vacancies for workers with work experience from 1 to 3 years.
Источник / Source: составлено авторами / compiled by the authors.
Действия работодателей на этом рынке хорошо согласованы и имеют устоявшуюся структуру. Стоит отметить, что без опыта работы требуются рабочие только на стандартный способ занятости, на вахту работодатели готовы нанимать только опытных рабочих.
К тому же было получено, что статистика публичных вакансий рабочих без учета вахты с опытом работы от 3 лет имеет схожую структуру со статистикой вакансий с опытом от 1 года до 3 лет. Объединенная статистика вакансий рабочих с опытом работы без учета вахты имеет показатель нерациональности ω=0.049. При этом после исключения из статистики промежутка с мая 2020 г. по декабрь 2020 г. показатель нерациональности снижается до уровня ω=0.015. Поэтому рынок та ких рабочих можно описать действиями одного рационального репрезентативного агента, а избы точный уровень нерациональности объясняется изменениями, связанными с шоковым событием – началом пандемии.
На рис. 9 видим, что за промежуток с 2018 г. по 2023 г. нижняя граница предлагаемой зарплаты рабочим с опытом выросла в 2,1 раз, с 23,6 тыс. до 48,8 тыс. руб. При этом зарплата рабочим без опыта росла более медленными темпами, в 1,9 раз, с 19,1 тыс. до 36 тыс. руб. Из динамики индексов количества вакансий (рис. 10) наблюдаем рост спроса на рабочих с опытом работы, примерно в 2 раза с 2018 г. При этом количество вакансий рабочих без опыта работы выросло незначительно, примерно на 25%.
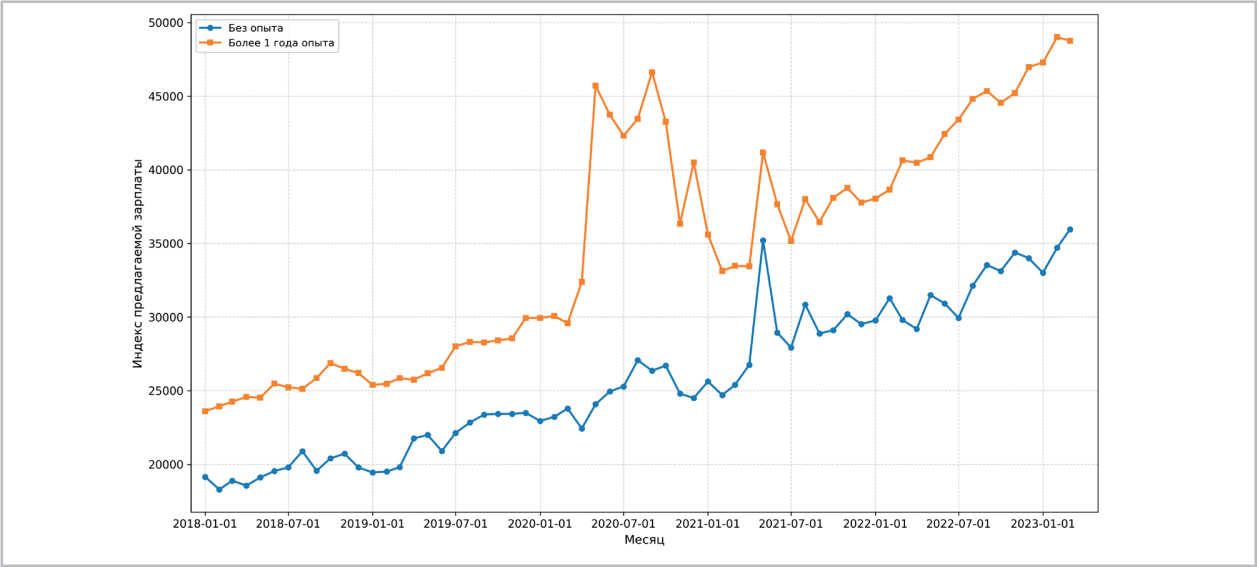
Рис. 9 / Fig. 9. Индекс предлагаемой зарплаты для рабочих стандартным методом работы в зависимости от требуемого опыта работы / Index of the proposed salary for standard method workers based on required work experience.
Источник / Source: составлено авторами / compiled by the authors.

Рис. 10 / Fig. 10. Индекс количества вакансий для рабочих стандартным методом работы в зависимости от требуемого опыта работы / Index of the number of vacancies for standard method workers based on required work experience.
Источник / Source: составлено авторами / compiled by the authors.
Рынок публичных вакансий рабочих без опыта оказался устойчив к пандемии, темпы роста предлагаемой заработной платы сохранились на прежнем уровне. Такой же результат отражает по казатель нерациональности статистики, он оказался довольно низким без исключения каких либо периодов.
Пандемия отразилась на рынке публичных вакансий рабочих с опытом. Изменилась структура поведения предприятий, их действия с мая по декабрь 2020 г. нельзя описать одним рациональным репрезентативным агентом. Однако с начала 2021 г. ситуация стабилизировалась, структура поведения предприятий на рынке публичных вакансий осталась аналогичной, как была до пандемии.
Стоит отметить, что опытный рабочий при по иске работы невахтовым методом может рассматривать вакансии, не требующие опыта работы, и может сделать выбор в их пользу в зависимости от условий и оплаты труда. Поэтому рационализируемую группу публичных вакансий рабочих без опыта работы стоит рассматривать, как опцию к вакансиям рабочих с опытом. В рамках модели к статистике вакансий с опытом работы от 1 года была добавлена еще одна типовая позиция в виде индекса предлагаемой зарплаты и количества вакансий статистики рабочих без опыта работы. Такая расширенная статистика имеет по казатель нерациональности ω=0.062, являющийся довольно высоким. Однако показатель нерациональности может быть снижен до уровня ω=0.015 путем исключения из статистики промежутка после начала пандемии, с мая по декабрь 2020 г. Та ким образом, группа вакансий рабочих стандартным методом работы может быть описана одним репрезентативным агентом в периоды, отличные от исключенных. В пандемийные месяцы 2020 г. рынок вакансий без вахты оказался неустойчив, однако с начала 2021 г. структура вернулась в прежнее состояние.
Для вакансий рабочих вахтовым методом ситуация иная. Статистика рабочих на вахте оказалась нерационализируемой, ее показатель нерациональности составляет ω=0.048. Выделение несогласованных периодов и их исключение существенно не снижает уровень показателя нерациональности. Это означает, что вахту средней группы регионов нельзя рассматривать как отдельный полный класс вакансий. Это может объясняться тем, что одно и то же место на вахте может предлагаться работникам из регионов с разным уровнем доходов населения. К тому каждый рабочий, рассматривающий работу на вахте, имеет варианты с работой по месту своего проживания. Далее последнее замечание было учтено в модели.
К статистике рабочих на вахте предлагается добавить еще одну типовую позицию, представляющую собой индекс предлагаемой зарплаты и количества вакансий для рабочих без вахты. По лученная статистика описывает варианты, предлагаемые опытным рабочим для дальнейшей работы. Показатель нерациональности статистики составляет ω=0.096. Избыточная нерациональность объясняется изменениями, произошедши ми с начала пандемии, в периоды с мая по октябрь 2020 г., в декабре 2020 г., а также в апреле 2022 г. и в феврале-марте 2023 г. Исключение статистики за эти месяцы привело к снижению показателя нерациональности до уровня ω=0.022.

Рис. 11 / Fig. 11. Структура рынка публичных вакансий рабочих в средней группе регионов / Structure of the market for public vacancies of workers in the middle group of regions.
Источник / Source: составлено авторами / compiled by the authors.
Итоговая модель для рынка публичных вакансий рабочих для регионов со средним уровнем доходов изображена на рис. 11. Группа вакансий рабочих без опыта работы отделима от группы вакансий рабочих со стандартным методом работы. В свою очередь, группа вакансий рабочих со стандартным методом работы отделима от всех вакансий рабочих. Человек без опыта работы, же лающий занять позицию рабочего, вынужден работать по месту своего проживания, опция с вахтовым методом для него недоступна. Для рабочего, имеющего опыт работы, имеется более широкий круг вакансий, а также появляется вариант с трудоустройством вахтовым методом, что предполагает более высокий уровень оплаты труда (рис. 12).
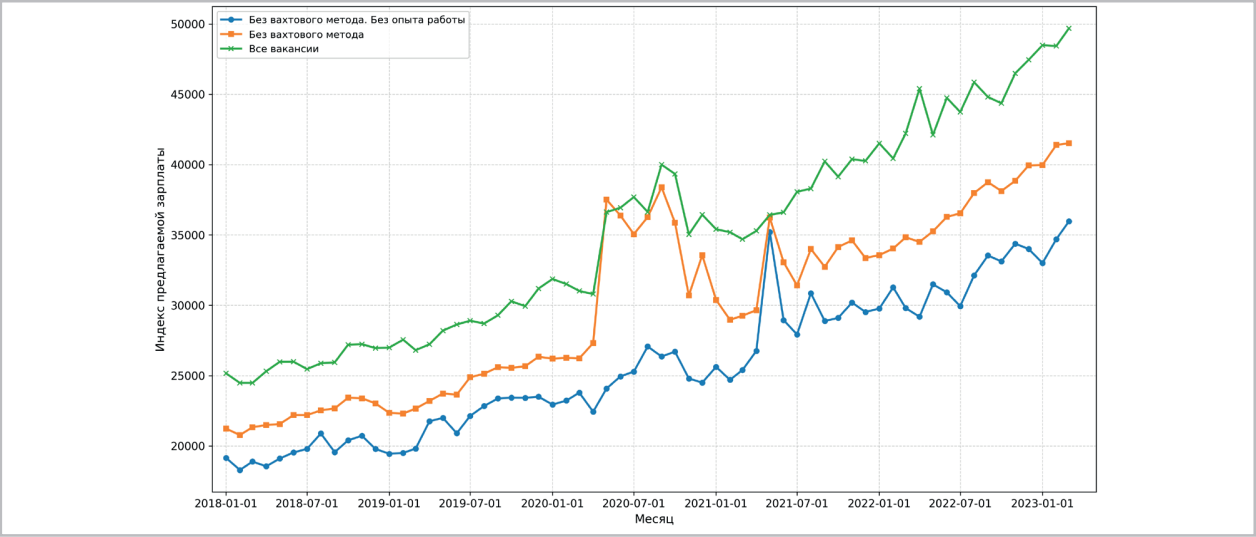
Рис. 12 / Fig. 12. Вложенные индексы предлагаемой зарплаты для рабочих средней группы регионов / Nested indices of the proposed salary for workers in the middle group of regions.
Источник / Source: составлено авторами / compiled by the authors.
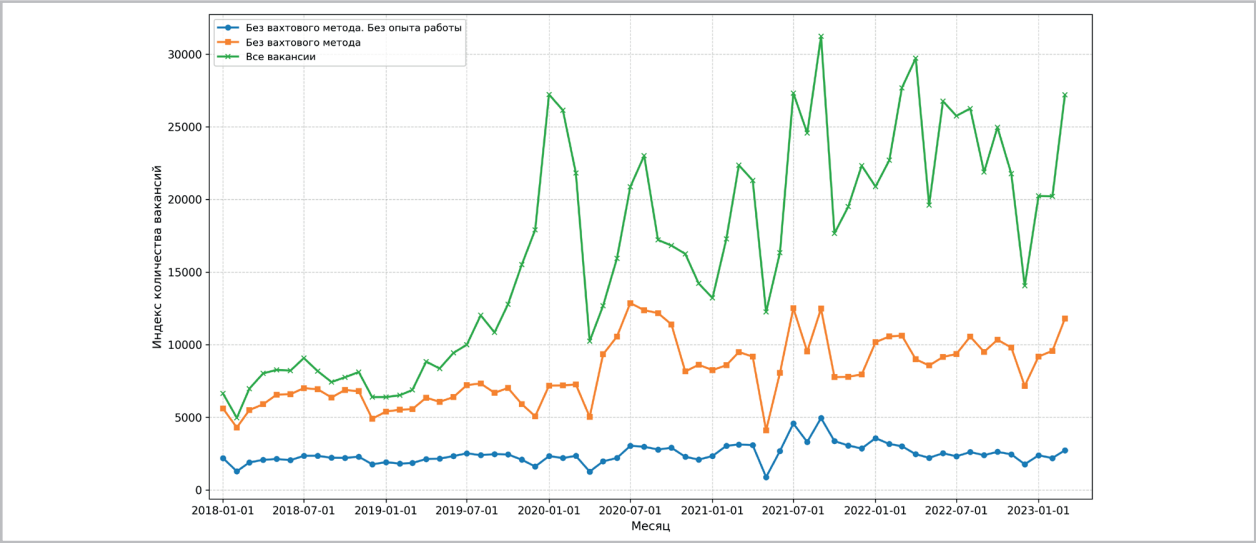
Рис. 13 / Fig. 13. Вложенные индексы количества вакансий для рабочих средней группы регионов / Nested indices of the number of vacancies for workers in the middle group of regions.
Источник / Source: составлено авторами / compiled by the authors.
Действия предприятий на рынке вакансий рабочих без опыта хорошо согласованы между собой и описываются одним репрезентативным агентом, предпочтения которого сохранились во время пандемии. Рынок публичных вакансий рабочих без вахтового метода работы также представляет из себя группу согласованных и взаимодополняющих вакансий, но его структура оказалась неустойчива к влиянию пандемии, что отразилось ростом спроса на рабочих (рис. 13) с повышением предлагаемой зарплаты (рис. 12). Работа вахтовым методом вписывается в общую структуру рынка рабочих и предоставляет альтернативу для опытных работников.
Непараметрический метод предоставляет удобный инструмент идентификации изменений на рынке публичных вакансий. Метод выделения несогласованных периодов и анализ показателя нерациональности статистики без какой-либо дополнительной информации об исследуемой стати стике позволяет выделять временные точки, в которые сложившаяся структура рынка нарушалась. Для рынка публичных вакансий рабочих, имеющих опыт работы, было обнаружено, что начало пандемии изменило поведение предприятий. Работодатели повысили предлагаемую зарплату, чтобы закрыть потребность в опытных рабочих. При этом с начала 2021 г. предпочтения стабилизировались и вернулись к структуре, сложившейся до пандемии.
В рамках работы был разработан подход для оценки премии работникам за трудоустройство и работу в условиях изменений, связанных с шоковыми событиями. В период пандемии для рабочих с опытом от 1 года до 3 лет предлагаемая зарплата была завышена до 30%. При этом для некоторых типовых позиций рабочих дефицит сотрудников отразился незначительно, уровень предлагаемых зарплат согласуется с данными до пандемии.
Непараметрический метод позволяет выделять отделимые группы вакансий и строить экономические индексы предлагаемой зарплаты и количества вакансий, учитывая эффекты замещения и перетоков работников с одних типовых позиций на другие, требующие схожую квалификацию и предлагающие более привлекательные условия труда. Построенные индексы отражают ситуацию на рынке публичных вакансий и удобны для интерпретации и принятия социально экономических решений.
Разработанные подходы особенно актуальны в условиях дефицита работников, с которым столкнулся российский рынок труда в 2023 г.
Работа выполнена при финансовой поддержке РНФ, грант №23-21-00281.
Андрей Сергеевич Куць – эксперт ФГБУ «ВНИИ Труда» Минтруда России, математик ФИЦ ИУ РАН, аспирант МФТИ (НИУ), Москва, Россия.
Владимир Иванович Джума – директор Центра цифровой трансформации и анализа данных, ФГБУ «ВНИИ труда» Минтруда России, Москва, Россия.
Материалы данной статьи не могут быть использованы, полностью или частично, без разрешения редакции журнала «Социально-трудовые исследования». При цитировании ссылка на ФГБУ «ВНИИ труда» Минтруда России обязательна.